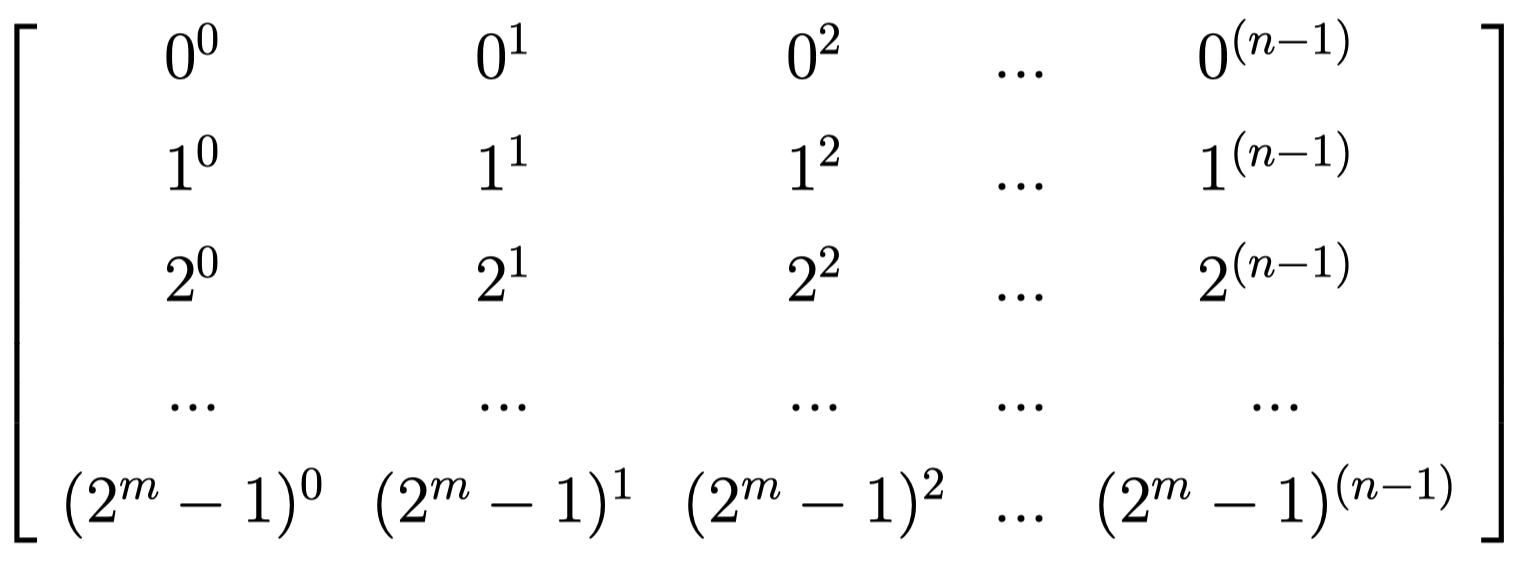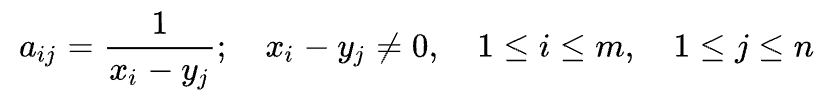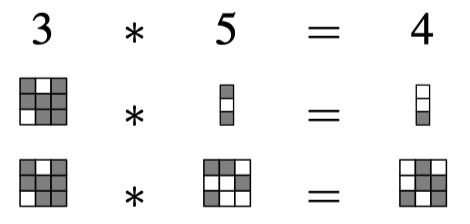Post

RS码原理及柯西优化

Posted Updated
By Evan 17 min read

Intro

Forward Error Correction（前向纠错、FEC）技术可以用于在不可靠信道中传输信息，当信道中发生丢包时通过部分原始和对应的冗余信息恢复出全部的原始信息。举例来讲，数据块 a 和 b 生成了冗余数据块 c ，在接收端只收到 a 和 c 时，能够还原出原始数据块 b，省去了请求和响应重传的时间。

Reed–Solomon Error Correction（RS码、里所码）是一种FEC算法，假设原始和冗余信息块数量分别是 n 和 k，在接收端任意收到 n 个原始/冗余信息块时，通过RS解码都能还原出 n 个原始数据块。回到上文的例子，如果使用 a 和 b 这两个原始数据块（n=2），生成 c 和 d 两个冗余数据块（k=2），使用XOR操作时无法保证任意2个数据块到达后都能恢复出 a 和 b，而RS码可以保证。

本文将主要基于 An Introduction to Galois Fields and Reed-Solomon Coding1 和 Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Network Storage Applications2 介绍RS码基本原理及柯西优化的相关内容。

伽罗瓦域

1. Feild（域）

Field（域）是加法和乘法运算被定义的元素集合，其中的元素和定义的运算满足以下性质：

  1. 两个元素进行加法和乘法运算后的结果还在域内（closure闭包性质），定义在域的加法和乘法运算都满足交换律和结合律
  2. 域拥有加法元和乘法元: 0+a=a, 1*a=a
  3. 定义了加法逆（减法）和乘法逆（除法）
  4. 加法元$\neq$乘法元
  5. ab=0 <=> a=0 or b=0

实际上在后续的介绍中，域的加法和乘法运算的闭包性质是最为重要的，其他性质能够协助一些原理推导。另外域的元素应理解为“存在”，而域内的加法/乘法运算应理解为“定义”，比如 $(a+b)\%N$ 和 $a\oplus b$都应该被理解为“加法运算”。

2. Finite Field（有限域）

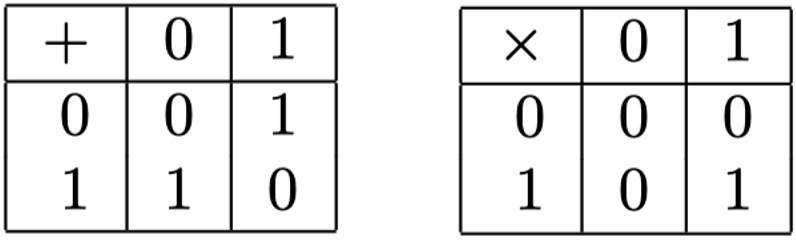
Finite Field（有限域）即元素有限的域。常见的有限域有定义在模除运算p（p为质数）上的 $ℤ_{p}$，其元素为{0,1,2,…,p-1}，加法运算为 $(a+b)\ mod\ p$，乘法运算为 $ ab\ mod\ p $。

以下是$ℤ_{2}$的加法表和乘法表：

add-multi

3. Galois Field（伽罗瓦域）

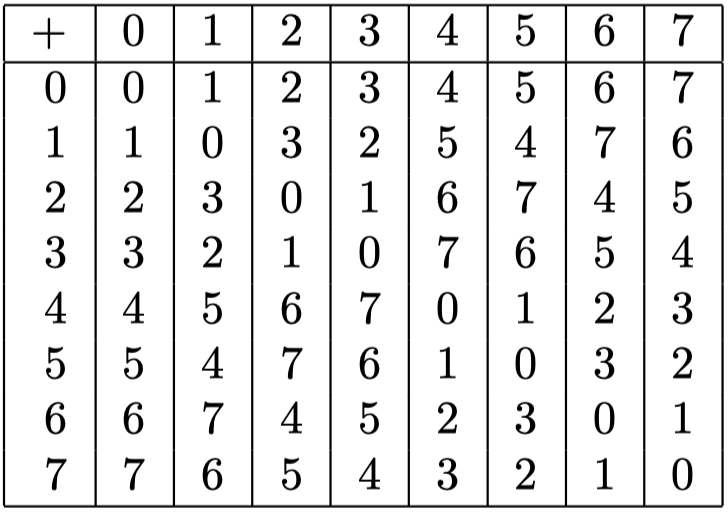
Galois Field（伽罗瓦域）使用符号$GF(p^m)$表示，其元素是定义在$ℤ_{p}$上的m-1次多项式。展开后为 $a_{m-1}x^{m-1} +…+ a_{1}x^1 + a_{0}x^0$，其中系数 $a_{i}$ 取自集合{$0, 1, …, p-1$}。在编码中我们常取p=2，此时m-1次多项式表达一个长度为m位的字，当m=8时则表示一个字节。

PS：以下带*的小章节可以不做理解

a. 加法运算

伽罗瓦域上的加法为对多项式逐位进行异或：$(x^2+1)+(x+1)+(x^2+x+1)=1$，根据异或的特性可以知道，加法的逆运算减法实际上也是逐位进行异或。

以下是 $GF(2^3)$ 的加法表：

add-gf-2-3

b. 乘法运算

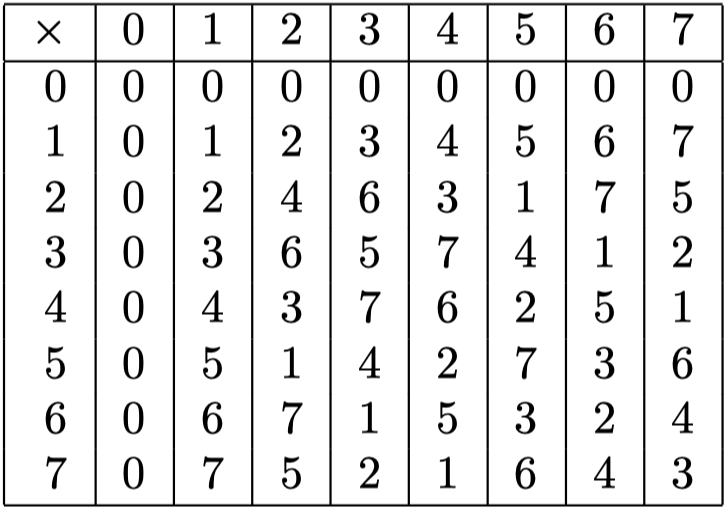
伽罗瓦域$GF(2^m)$的最高次限制为m-1，但乘法的直接结果可能超过这个值。下式中为 $GF(2^3)$ 的乘法运算，结果的最高位已经超过m-1=2

$5\cdot6=(x^2+1)(x^2+x)=x^4+x^3+x^2+x$

因此，需要找到不可约多项式g(x)来使得乘法的结果回到域内，使得$p(x)=a(x)b(x)$在域外，但$f(x)=p(x)\ mod\ g(x)$又回到域内，这个思想有些类似 $ℤ_{p}$ 上乘法的模除 p 操作。

$x^3+x+1$ 是 $GF(2^3)$ 上的一个不可约多项式，以下为 $5\cdot6$ 的结果，使用 g(x) 将其模除回域内的过程，最终计算的结果为 $x+1$ 即 3：

multi-mod-gf-2-3

通过逐个计算，可以得到 $GF(2^3)$ 的乘法表：

multi-gf-2-3

c. 乘法函数*

以下是乘法的编程实现，分别模拟了竖乘和长除的过程，需要注意的是 $GF(2^m)$ 中的加减法都是逐位进行异或操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

int gf_mult(int m, int poly, int v1, int v2) {
  // poly: low order terms of g(x)
  int prod = 0; 
  int k; 
  int mask;
  /* Multiply phase */
  for (k = 0; k < m; k++)
  {
    // 通过移位和异或操作模拟竖乘的过程
    if (v1 & 1) {
      prod ^= (v2 << k);
    }
    v1 >>= 1;
    if (v1 == 0) break;
  }

  /* Reduce phase */
  // 当m=3，mask=10000，即上一步结果可能出现的最高位
  mask = 1 << (2m-2); 
  for (k = m - 2; k >= 0; k--)
  {
    // 通过移位mask模拟g(x)的长除过程
    if (prod & mask) {
      // 直接去掉当前最高位
      prod &= ~mask;
      // 长除上部写上1，做异或减法
      prod ^= (poly << k);
    }
    mask >>= 1;
  }
}

4. 快速乘法*

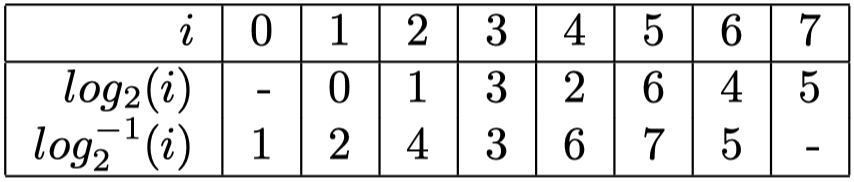
伽罗瓦域中的乘法可以借助对数运算实现，即 $a \cdot b=log_{2}^{-1}(log_{2}(a)+log_{2}(b))$ 成立，其中右式的“+”是自然数加法而不是多项式加法。下表是 $GF(2^3)$ 上的对数表：

log-gf-2-3

其中需要注意以下问题：

  1. 表中的所有单元格内都是遍历整个 $GF(2^3)$ 中所有元素尝试出来的，没有更快的生成方法
  2. 表中有两个不定义的项，不定义的原因在此不做展开，可以参考1
  3. $log_{2}^{-1}(7)$ 未定义：7减7后为0，$log_{2}^{-1}(0)=1 => 3\cdot6=1$
  4. $log_{2}(0)$ 未定义：$0\cdot n=0 => 0$，不需要使用快速乘法

快速乘法表的生成较慢（因为需要遍历），但生成后能够大幅度提高乘法的运算速度，可以作为RS码编码的一种优化方案。

RS码

范德蒙特矩阵

Vandermonde（范德蒙特）矩阵是一种 m 行 n 列的特殊矩阵，它的第 i 行第 j 列的元素 $V_{i,j}=\alpha_{i}^{j-1}$，任意 n 行组成的 $n\times n$ 子矩阵都是满秩方阵（即能够求得逆矩阵）。在 $m>n$ 时，能够通过行之间的线性变换将范德蒙特矩阵的前 n 行变为单位矩阵，且依然保持任意 $n\times n$ 子矩阵满秩。下图是 $GF(2^m)$ 上的范德蒙特矩阵，$\alpha_{i}$ 的取值是 $GF(2^m)$ 上所有的 $2^m$ 个元素，次方乘法遵守伽罗瓦域上的乘法定义。

Vandermonde

RS编码

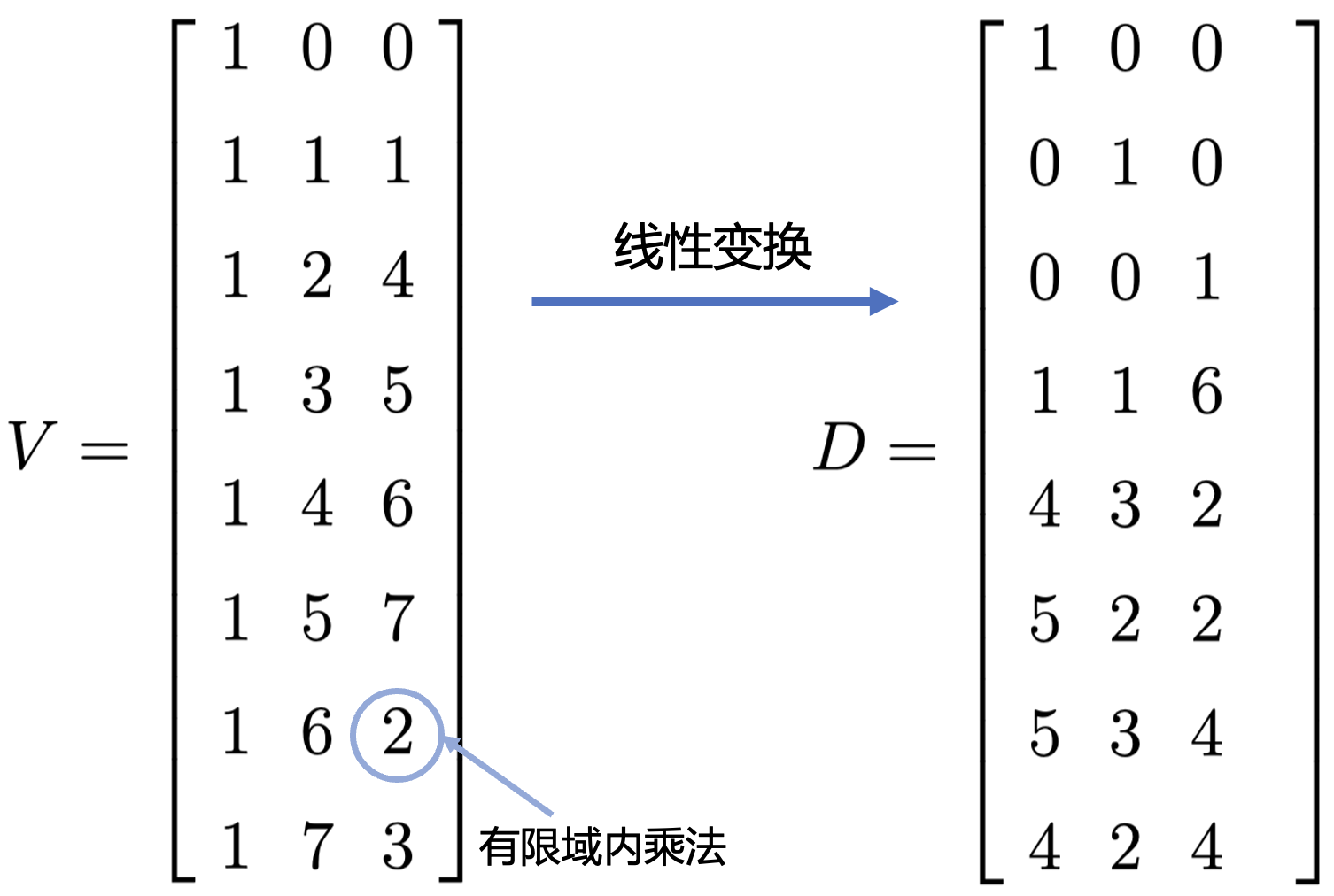
RS编码可以使用范德蒙特矩阵作为生成矩阵，下图左侧是 $GF(2^3)$ 上的范德蒙特矩阵$V$，经过线性变换后得到右侧的分布矩阵$D$。矩阵$D$有两个主要特征：1. 前n行是单位矩阵， 2. 任意 $n\times n$ 子矩阵满秩。

vandermonde-generate-matrix

RS编码时将分布矩阵$D$与原始数据向量相乘，得到一个同时包含原始和编码数据的新向量，解码时原始和编码数据块达到数目后（此例中是5个），就可以恢复出所有的原始数据。这种原始数据保持不变的编码也被称为“系统性编码”3，它的好处是接收端获得的所有原始数据都能够直接使用。

rs-encode

总结RS编码过程可以发现以下特征：

  1. 逐组进行编码：编码过程中的矩阵相乘需要有一定长度的原始数据向量才能进行。当原始数据处于持续产生的过程中时，有可能同组的第一个和最后一个原始数据生成时间差距较大，此时RS编码器只能等待
  2. 位置关系：同组的原始/编码数据块都需要标明它在组内的位置，这部分的原因会在解码部分详述
  3. 组的极限长度：每个RS编码组内的数据块个数也是有限的。分布矩阵$D$的最大行数 == $GF(2^m)$的元素个数 == $2^m$，所以每个编码组的原始+编码数据块个数最大也是$2^m$。在实际的代码实现中，$GF(2^8)$因为每个元素都能表达一个字节的数据而被广泛使用，在这种情况下每个编码组的原始+编码数据块限制为256

RS解码

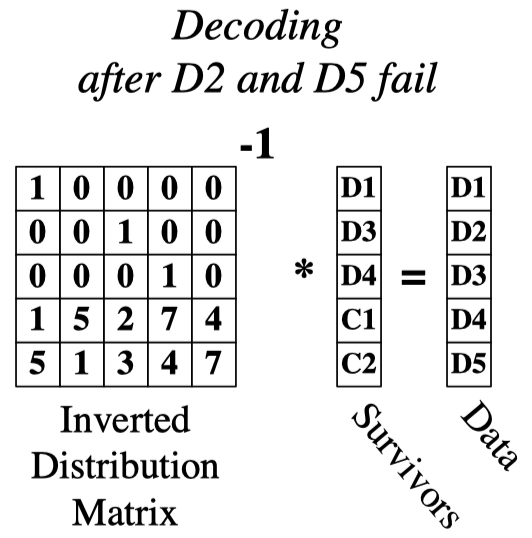
RS解码的条件是“收到的原始+编码数据块数目>=原始数据块数目”，信道中的丢失过程等价于在编码时抽去矩阵$D$的一部分行。下图是在$D_{2}$和$D_{5}$丢失的情况下，RS解码的过程，左侧的等价生成矩阵实际上就是编码过程中抽去矩阵$D$的第2和5行。在进行解码时，要对这个$n\times n$矩阵求逆，与获得的数据向量相乘后还原出原始数据。

rs-decode

从解码过程获得等价分布矩阵的过程可以看出，接收端必须确定从原始的矩阵$D$中抽去哪些行，所以所有原始/编码数据块都需要标明自己在组内的位置。并且在进行协议设计时，也要避免组间出现重叠，即收到一个原始/编码数据块后，要能够明确它是属于哪个编码组的。

柯西优化

柯西优化主要利用了柯西矩阵相较于范德蒙特矩阵求逆更快的特点，获得了更高的编解码效率。由于需要逐字节分割数据，之前介绍的RS编码在$GF(2^m)$中常将m取8、16和32这种整值。但是在以下的优化中，通过对于数据的向量/矩阵表示，m的取值可以不再整除8，比如取m=3，这样编码组的大小能够更加灵活。

柯西矩阵

柯西矩阵有跟前文所述范德蒙特矩阵作为分布矩阵时类似的两个主要特征：1. 可以通过线性变换将前n行变为单位矩阵，2. 任意 $n\times n$ 子矩阵满秩。柯西矩阵中的元素$a_{i,j}$如下：

cauchy-element

在理解RS码时将范德蒙特矩阵和柯西矩阵等价即可，柯西矩阵的求逆复杂度是$O(nlog_{2}(m+n))$，其中n是原始数据块个数，m是编码数据块个数。

向量/矩阵表达

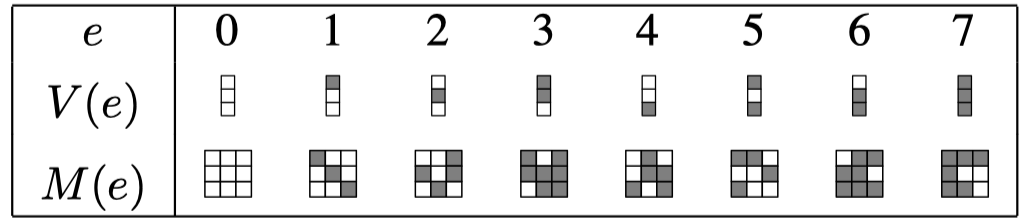
在 $GF(2^m)$ 上，可以将元素表达为向量和矩阵形式，其中向量就是它们的多项式表达形式，矩阵表达形式$M(e)$的第i列为$V(e2^{i-1})$。

caucy-vector-matrix-element

如此一来，$GF(2^m)$上的乘法可以转变为纯粹的XOR操作。下图中将 5 的向量表达设为 {$d_{0},d_{1},d_{2}$}，相乘结果 4 的向量表达为 {$e_{0},e_{1},e_{2}$}，则 $e_{0}=d_{0}\oplus d_{2}$, $e_{1}=d_{0}\oplus d_{1}\oplus d_{2}$, $e_{2}=d_{1}\oplus d_{2}$。这种相乘实际上等同于伽罗瓦域上的竖乘过程，只是通过特殊的数据表达将所有操作转换为XOR操作。

cauchy-multiply

编码结构优化

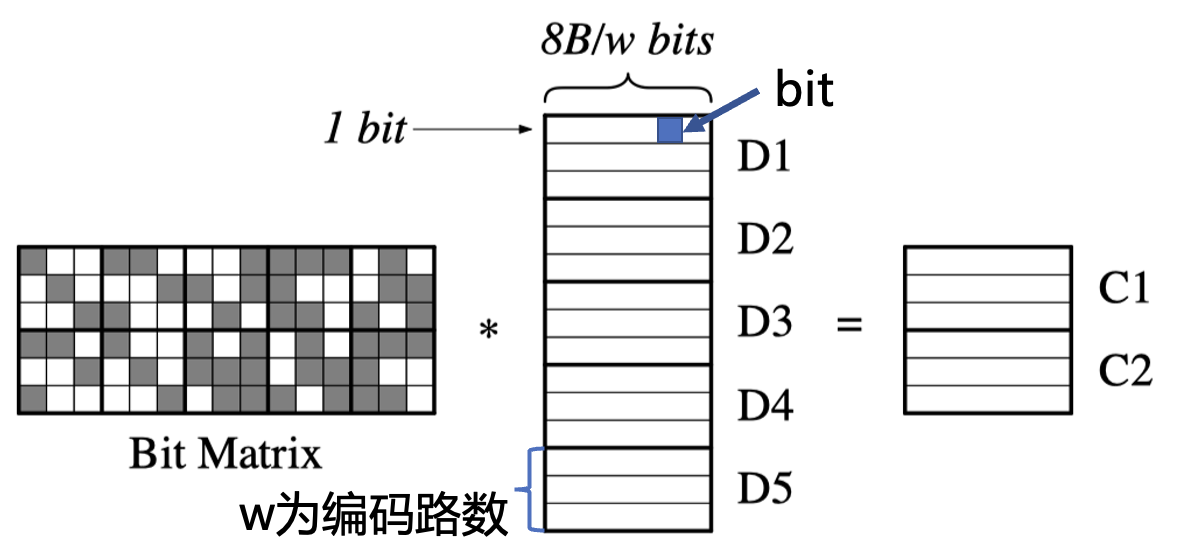
在柯西优化的编码结构中，编码的基本单位是 bit 而不再是 byte（m=8bit），重新定义 $GF(2^w)$ 作为编码的基础伽罗瓦域，其中w还是每个元素的长度，对应到上一部分的向量/矩阵即为它们的行数。但在实际的编码结构中，分布矩阵$V$已经使用点阵表达，原始数据向量也被以bit为单位拆分，其他编码和解码原理不变。

cauchy-encode

编码结构的变化主要来自于数据表达方式的改变，但是带来的主要区别只有 $GF(2^m)$ 中m的取值范围，比如柯西优化中可以取3。

进一步优化

数据表达方式变化后，编解码复杂度直接取决于分布矩阵中的bit数，即bit matrix中黑格的数目。实际上编码使用的柯西矩阵也有区别，分布矩阵更少的bit数能提高编解码效率，具体的优化参见2。

Ref

  1. An Introduction to Galois Fields and Reed-Solomon Coding ↩ ↩2

  2. Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Network Storage Applications (使用第一页说明中的12页版本) ↩ ↩2

  3. 系统性编码 Systematic code Wikipedia ↩

数理基础
前向纠错 线性代数 FEC
This post is licensed under CC BY 4.0 by the author.